
Karnaugh Map (K-Map) in Digital Electronics
The Karnaugh Map (K-map) is a visual method for simplifying Boolean algebra expressions. It reduces complex Boolean expressions, making it easier to design efficient digital circuits.
By organizing truth table values in a grid, the K-map allows us to group terms and simplify them based on the rules of Boolean algebra.
Why Use a K-map?
When working with Boolean functions in digital electronics, simplifying the logic expression is essential to minimize the number of gates and wiring.
A truth table can represent all possible inputs and corresponding outputs, but simplifying that into a manageable form manually can be difficult.
A K-map makes it easier to spot common patterns and quickly reduce an expression.
Structure of a K-map
A K-map is a rectangular grid where each cell represents a minterm (in Sum of Products) or a maxterm (in Product of Sums).
The size of the K-map depends on the number of variables in the Boolean function:
- 2 variables: 4 cells (2^2)
- 3 variables: 8 cells (2^3)
- 4 variables: 16 cells (2^4)
Each cell corresponds to a combination of variables' values (either 0 or 1) and is arranged in Gray code order.
Gray code ensures that any two adjacent cells differ by only one variable, making it easy to group them.
2-Variable K-map
A 2-variable Boolean function involves two inputs, say A and B. The corresponding K-map looks like this

- m0 corresponds to A'B'
- m1 corresponds to A'B
- m2 corresponds to AB'
- m3 corresponds to AB
Example: 2-variable K-map
Consider the Boolean function: [ F(A, B) = Σ(1, 3) ]
This represents minterms 1 and 3.
These are the cells where F(A, B) = 1. We plot the values on the K-map

Now, group the 1s together. Here, m1 and m3 form a vertical group, allowing us to simplify the expression as: [ F(A, B) = B ]
3-Variable K-map
A 3-variable Boolean function involves three inputs, say A, B, and C. The K-map for three variables has 8 cells:

- m0 corresponds to A'B'C'
- m1 corresponds to A'B'C
- m2 corresponds to A'BC'
- m3 corresponds to A'BC
- m4 corresponds to AB'C'
- m5 corresponds to AB'C
- m6 corresponds to ABC'
- m7 corresponds to ABC
Example: 3-variable K-map
Consider the Boolean function: [ F(A, B, C) = Σ(0, 1, 5, 7) ]
This represents minterms 0, 1, 5, and 7. We plot these values on the K-map:

Now, group adjacent 1s. We can group m0 and m1, as well as m5 and m7, leading to the simplified expression: [ F(A, B, C) = A'B' + BC ]
4-Variable K-map
A 4-variable Boolean function involves four inputs, say A, B, C, and D. The corresponding K-map looks like this, with 16 cells:

Example: 4-variable K-map
Let’s simplify the Boolean function: [ F(A, B, C, D) = Σ(1, 3, 7, 11, 15) ]
Plotting these minterms on the K-map:
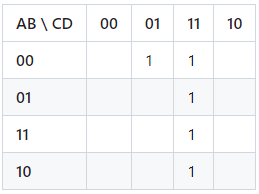
In this case, we can group m7, m11, and m15, as well as m1 and m3. The simplified Boolean expression is: [ F(A, B, C, D) = B'C + BD ]
Steps for Simplifying Using a K-map
- Plot the function: Identify the minterms (for SOP) or maxterms (for POS) from the Boolean function or truth table and place them in the K-map.
- Group adjacent cells: Group the 1s (for SOP) or 0s (for POS) in rectangles of size 1, 2, 4, or 8. Groups must contain powers of 2, and the larger the group, the simpler the expression.
- Simplify the expression: For each group, write down the Boolean expression, keeping only the variables that don’t change within the group. Combine these terms to get the final simplified function.
Advantages of K-maps
- Systematic and visual: K-maps provide a clear, visual method for Boolean expression simplification.
- Efficient minimization: It simplifies Boolean functions with fewer steps than algebraic methods.
- Error reduction: Helps to avoid errors that often occur during algebraic simplifications.
Limitations of K-maps
- Scalability: While K-maps are effective for up to 4 or 5 variables, handling more variables becomes challenging. For more than 5 variables, other methods like the Quine-McCluskey algorithm are often preferred.
- Human error: Manual grouping may lead to mistakes, especially with larger K-maps.
Conclusion
The Karnaugh Map (K-map) is a powerful tool for simplifying Boolean expressions, making it essential for digital logic design.
By plotting truth table values and grouping adjacent cells, the K-map reveals opportunities to minimize complex Boolean functions quickly and accurately.
The process of simplifying involves recognizing patterns that can reduce the number of gates needed in a circuit, saving cost and complexity.