Home

Home

Experts

Experts

Papers

Papers

Blogs

Blogs

Half, Full and Parallel adder in COA

Half, Full and Parallel adder in COA

What is a Half Adder?

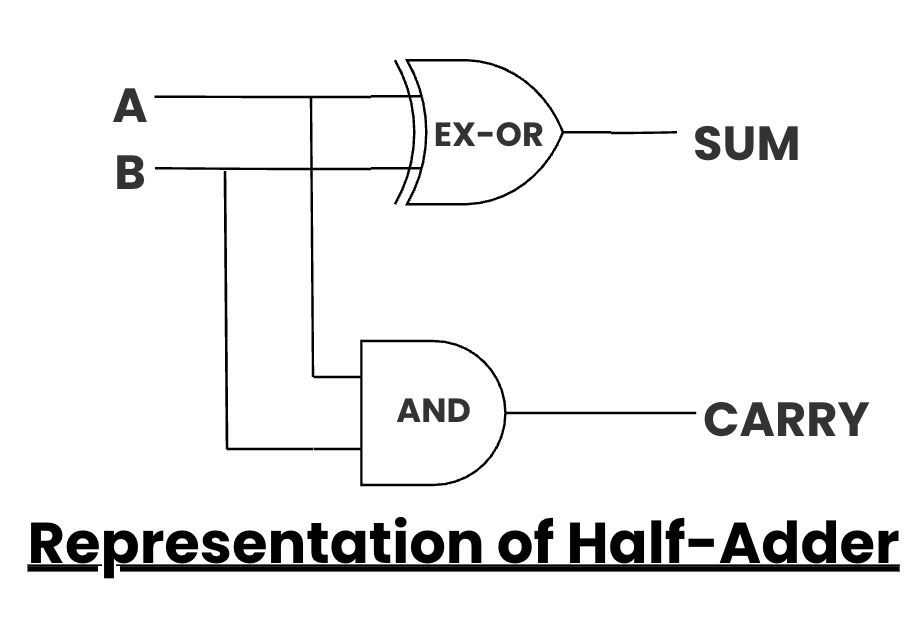
  • A half-adder is a fundamental building block in digital logic that adds two binary numbers.
  • It can handle only two inputs and produces two outputs: the sum and the carry.

How Does a Half Adder Work?

1. Input

  • The half-adder takes two binary inputs, typically labeled as A and B.
  • These inputs can be either 0 or 1.

2. Sum Output (S)

  • The sum output (S) represents the least significant bit of the addition result.
  • It is obtained by performing an XOR (exclusive OR) operation on inputs A and B.
  • The XOR operation results in 1 when the inputs are different and 0 when they are the same.

3. Carry Output (C):

  • The carry output (C) represents the carry bit generated during addition.
  • It is obtained by performing an AND operation on inputs A and B.
  • The AND operation results in 1 only when both inputs are 1; otherwise, it's 0.
image

Example:

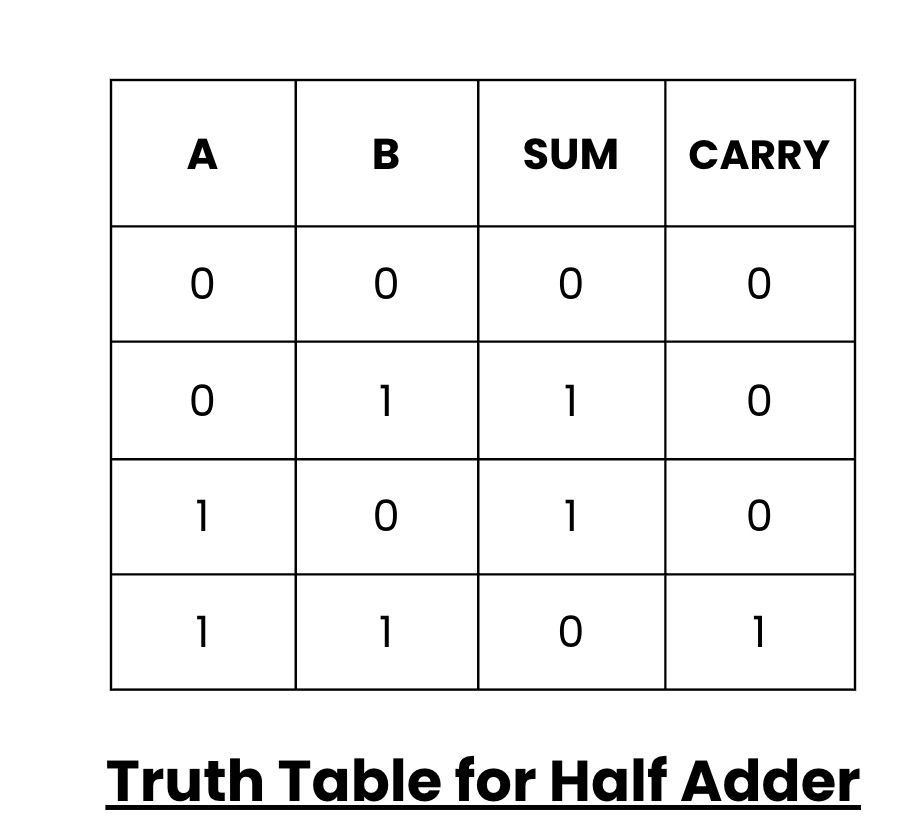
  • Let's say you want to add two binary numbers, A=1 and B=1, using a half adder.
  • Sum (S) = A XOR B = 1 XOR 1 = 0
  • Carry (C) = A AND B = 1 AND 1 = 1
  • So, the result is S=0 and C=1.
image
image

What is a Full Adder?

  • A full adder is an extension of the half adder, designed to handle three binary inputs: A, B, and an incoming carry (Cin).
  • It produces two outputs: the sum (S) and the carry out (Cout).

How Does a Full Adder Work?

1. Inputs:

  • The full adder takes three binary inputs: A, B, and Cin (carry-in).
  • A and B represent the binary numbers to be added, and Cin is the carry from the previous addition (initially, it's 0).

2. Sum Output (S):

  • The sum output (S) is calculated in two steps. First, it computes the sum of A and B, just like a half adder.
  • Then, it adds the carry input (Cin) to this sum. So, S = (A XOR B) XOR Cin.

3. Carry Out (Cout):

  • The carry-out (Cout) represents the carry generated by the addition of A, B, and Cin.
  • It's calculated by taking the carry-out of the first XOR operation (A XOR B) and the carry output of the AND operation between A and B.
  • Cout = (A AND B) OR ((A XOR B) AND Cin).
image

Example:

  • Let's add A=1, B=1, and Cin=1 using a full adder.
  • Sum (S) = (A XOR B) XOR Cin = (1 XOR 1) XOR 1 = 0 XOR 1 = 1
  • Carry Out (Cout) = (A AND B) OR ((A XOR B) AND Cin) = (1 AND 1) OR (1 XOR 1 AND 1) = 1 OR (0 AND 1) = 1 OR 0 = 1
  • So, the result is S=1 and Cout=1.
image

What is a Parallel Binary Adder?

A parallel binary adder is a combination of full adders used to add two multi-bit binary numbers simultaneously.

How Does a Parallel Binary Adder Work?

  • A parallel binary adder uses multiple full adders to add corresponding bits of the two binary numbers, starting from the least significant bit (LSB) and moving towards the most significant bit (MSB).
  • The carry-out of each full adder becomes the carry-in for the next full adder. This process continues until all bits are added.
Conclusion
half-adder is a basic digital circuit that adds two binary numbers. A full adder extends this concept to handle three inputs (A, B, and carry-in). Parallel binary adder employs multiple full adders.