
Hermite Curve in Computer Graphics
- The Hermite curve in computer graphics is an interpolation spline curve.
- Hermite curve was named after Charles Hermite, a French mathematician.
- The Hermite curve is defined by a set of control points and tangent vectors at those points.
Properties of Hermite Curve
- Interpolation: Hermite curves interpolate smoothly between their control points.
- Tangent Control: Hermite curves allow precise control over the tangent vectors at each control point.
- Parametric Representation: Hermite curves are often expressed as parametric equations, where a parameter u varies between 0 and 1.
- Derivatives: Hermite curves have continuous first and second derivatives.
- Local Control: Changes made to one segment of a Hermite curve affect only that segment, providing local control.
- Polynomial Form: The Hermite curve is expressed as a polynomial function, typically a cubic polynomial.
- Versatility in Applications: Hermite curves find applications in computer graphics, computer-aided design (CAD), animation, and modeling.
Hermite Curve Mathematical Expression

the above equation is very important we will use this equation in further steps below.
Let's Understand Hermite Curve Derivation
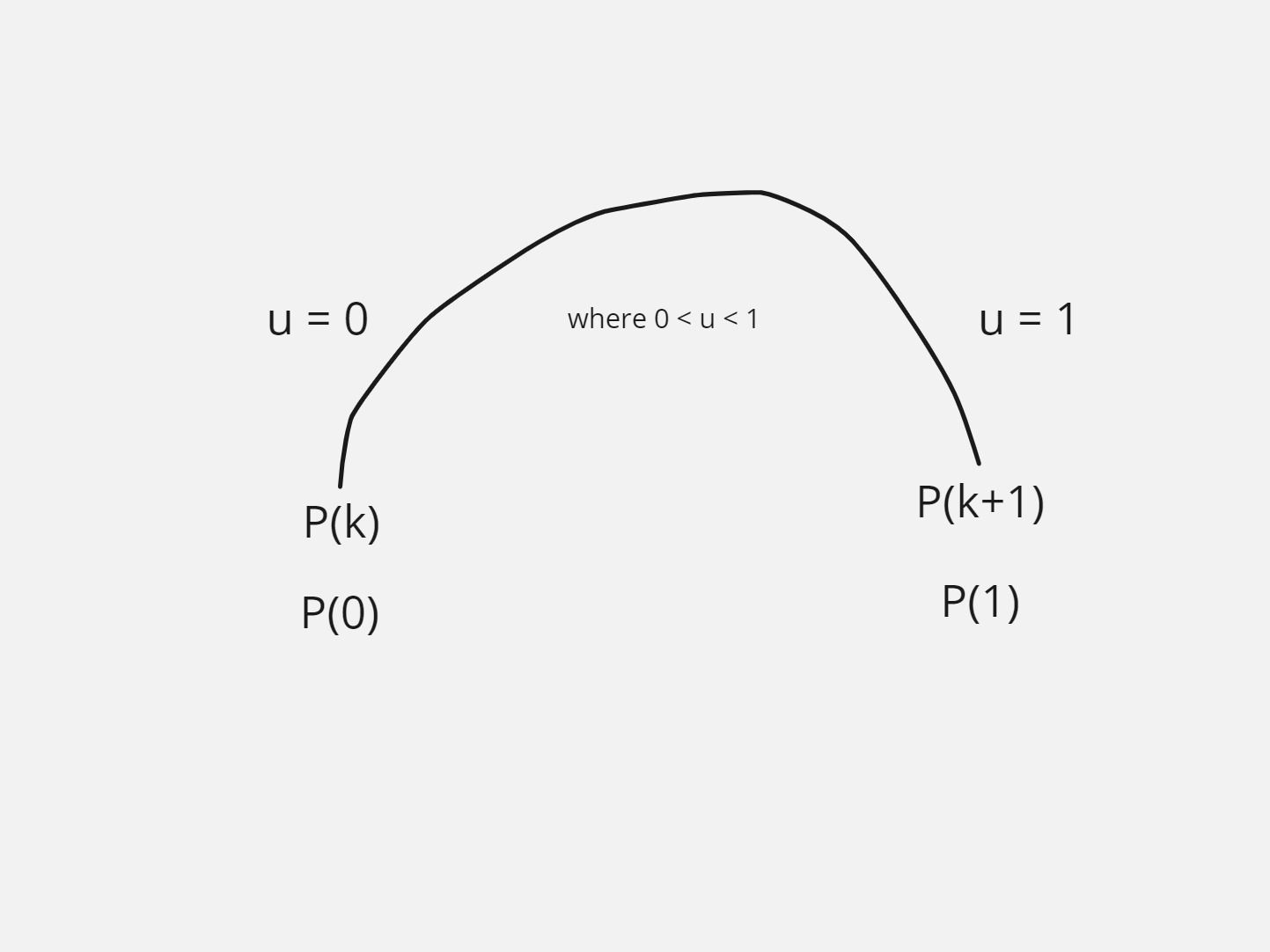
- In the above figure, we let two variables i.e. P (k) which is P(0), and P (k+1) which is P(1).
- Now we have to let the derivative of P(k) which is D Pk.
- and derivative of P(k+1) which is D Pk+1.
Now we have to find the derivative of the Hermite curve Mathematical Expression as follows:
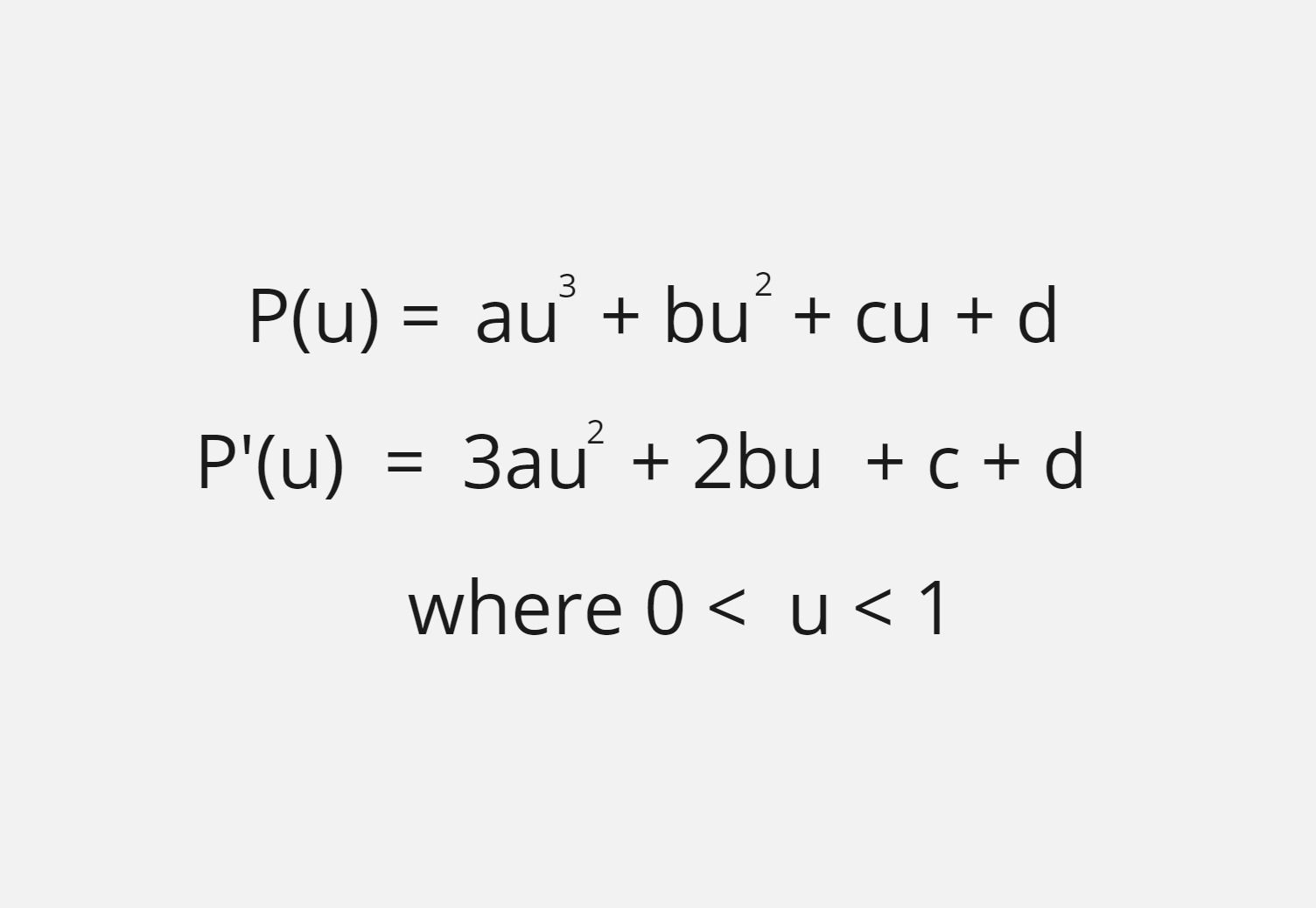
After finding the derivative of P(u) we need to put the values 0 and 1 in the u parameter in both the above equations as follows:
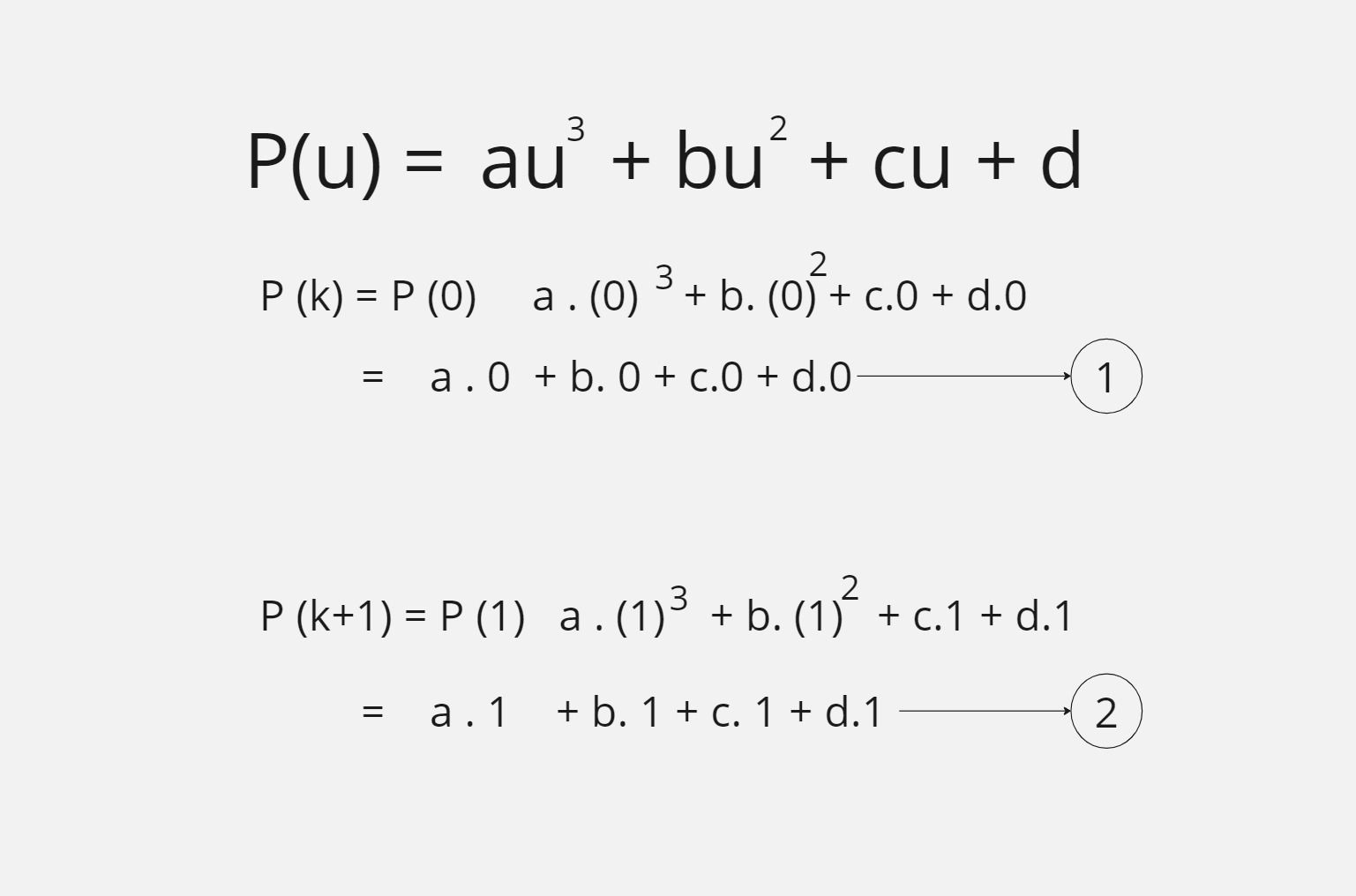
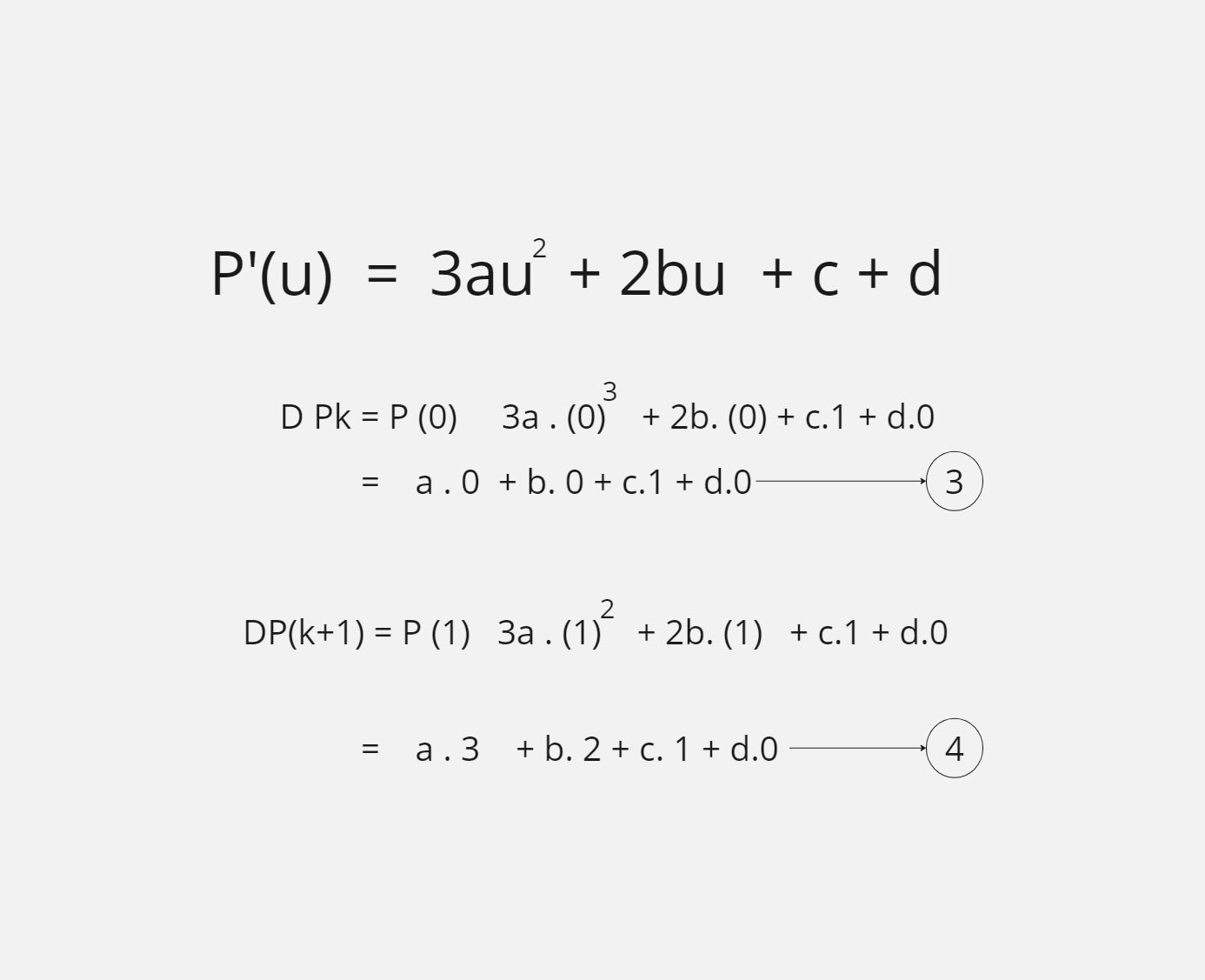
So after putting u as 0,1, we have 4 equations as follows:
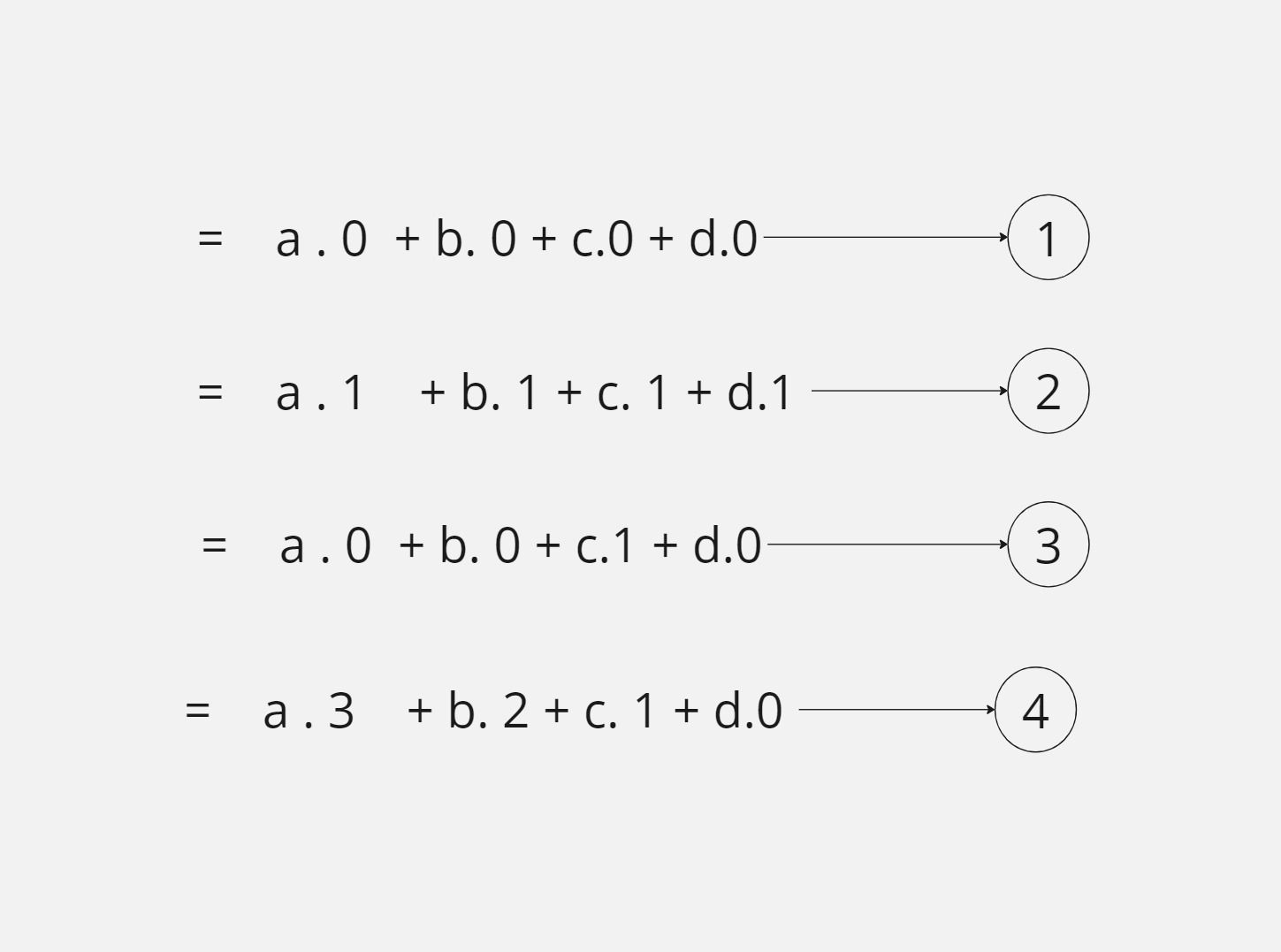
Now we have to represent these equations in terms of matrix as shown below so that we can find the Hermite matrix.

Now we can calculate the value of a, b, c by taking the inverse of the equation matrix.
The formula for calculating the inverse of the 4x4 matrix is A inverse= adj(A)/det(A).

So the above figure is a Hermite matrix after finding the Hermite matrix we need to multiply these two matrixes on the right side to find the value of a, b, c, d.

Hermite Blending Function
1P(k) h0 (u) + P(k+1) h1 (u) + DPK h2 (u) + DPk+1 h3(u)Advantages of Hermite Curves
Smooth Interpolation
- One of the primary advantages of Hermite curves is their ability to provide smooth interpolation between control points.
- This makes them suitable for creating aesthetically pleasing curves in graphical applications.
Conclusion
Understanding Hermite curves involves grasping their mathematical foundation and exploring practical applications.